BASICS
Physics of radiation detection
Electromagnetic radiation
The energy (E)and the frequency of the radiation quantum are calculable:
E = h* m h = 6,626*10-34
h = Planck's constant
Propagation speed can be calculated as well:
L = c / m c = 3*108 ms-1
c = speed of light
The spectrum of electromagnetic radiation ranges from alternating current to cosmic rays and contains in order of wavelength (long to short) longwave, shortwave, VHF, microwave, infrared, visible light, ultraviolet, x-ray, gamma ray and cosmic ray.

Evaluation Parameters
Irradiance
Irradiance marks the amount of radiant flux impinging on a unit surface area (per square meter). Unit:W/m².
In meteorology, irradiance constituted by sun and sky on a horizontal face in referred to as "global irradiance".
Illuminance:
is the counterpart of irradiance in light engineering and its measuring unit is Lux.
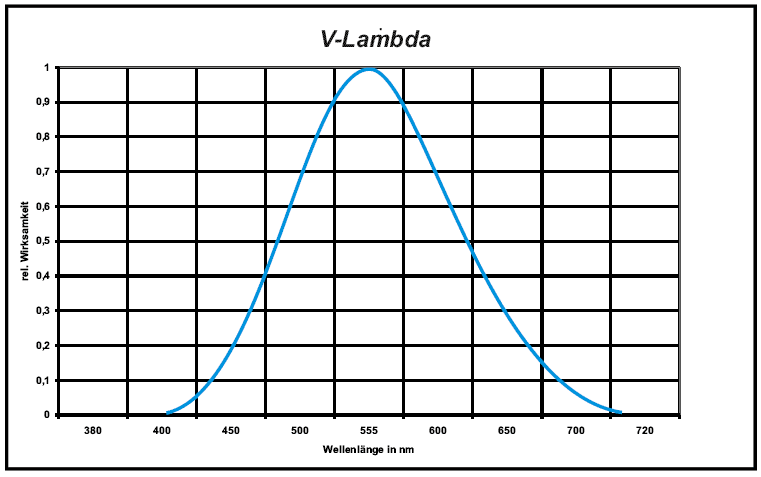
Measurement instrumentation in light engineering is only used for the range of visible radiation ( 380 nm - 780 nm). It's based on the physiological reception of radiation by the human eye. Curve progression of spectral effectivity is defined in the German DIN 5032.
Conversion into Irradiance is comparably complicated and has to be done by calculating the conversion factor 683 lm/W with the related spectral activity according to DIN 5032.
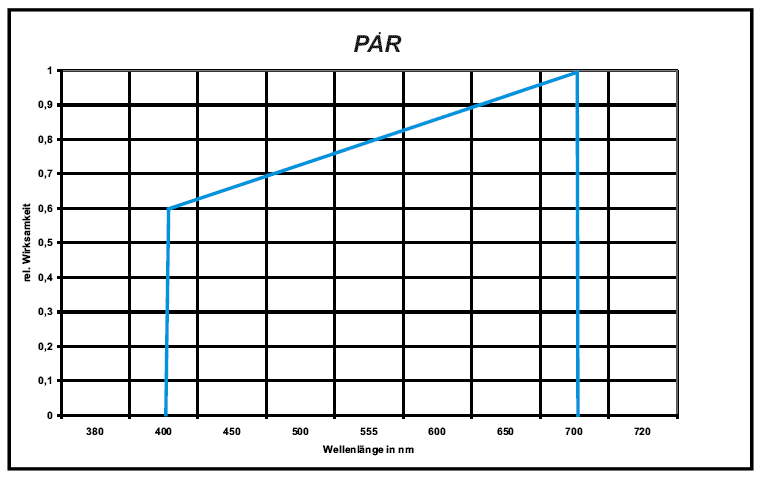
Photosynthetically active radiation
Photosynthetically active radiation (PAR) is normally quantified as µmol photons/m2/second. It designates the spectral range (wave band) of solar radiation from 400 to 700 nm. The spectral function is defined by the CIE (Commission internationale de l'Eclairage) as ideal quantum radiation.
Conversion is relating to the Avogadro constant (6.0022*1023 photons) with 1 mol= 1 einstein = 6.002*1023 photons. Conversion of spectral characteristics is similarly complicated.
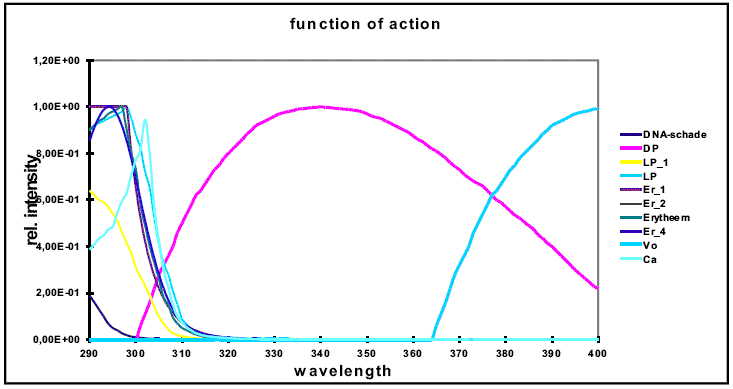
Action spectra
Besides eye sensitivity and PAR mentioned above there are other action spectra, of which some are pretty important:
Examples:
Carzinoma, vitamin-D-production, Caldwell, Erythema, skin pigmentation, PAR, Chlorophyll, and many others
The multitude of action spectra can only be implied here.
Important action spectra
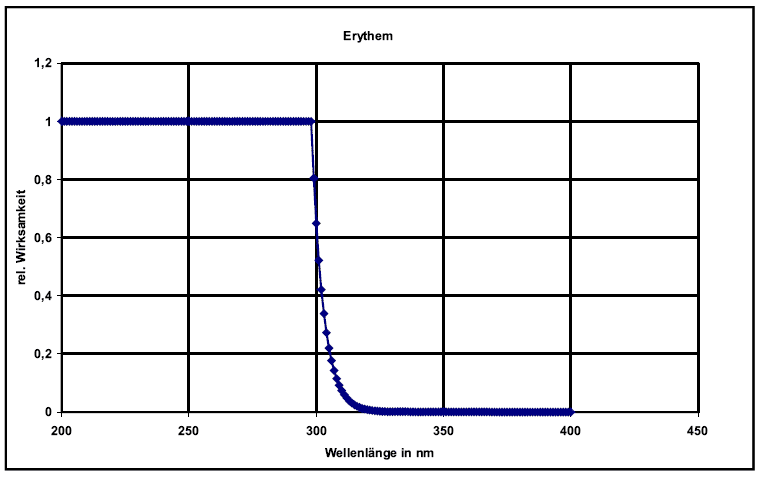
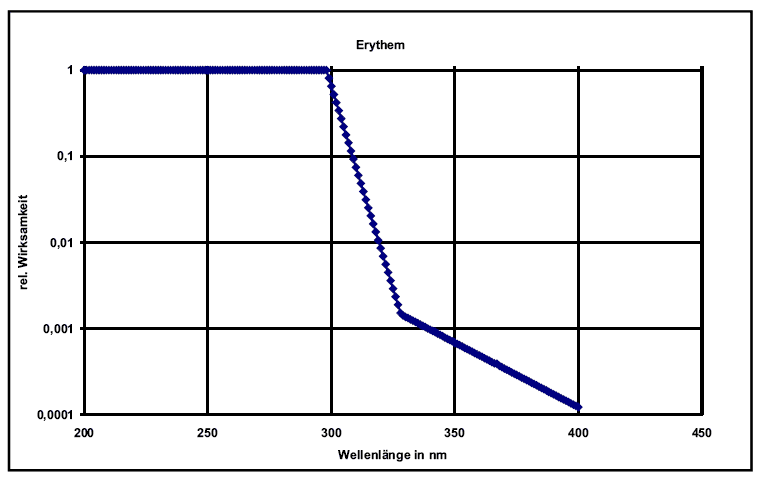
Erythema function
Among the best researched functions, and and the ones most discussed on international meetings, are those which pose a risk to humans when radiation is too intense.
Since a number of functions are bad for human skin these have been summarized into a single one recommended by CIE and published under DIN 5050.
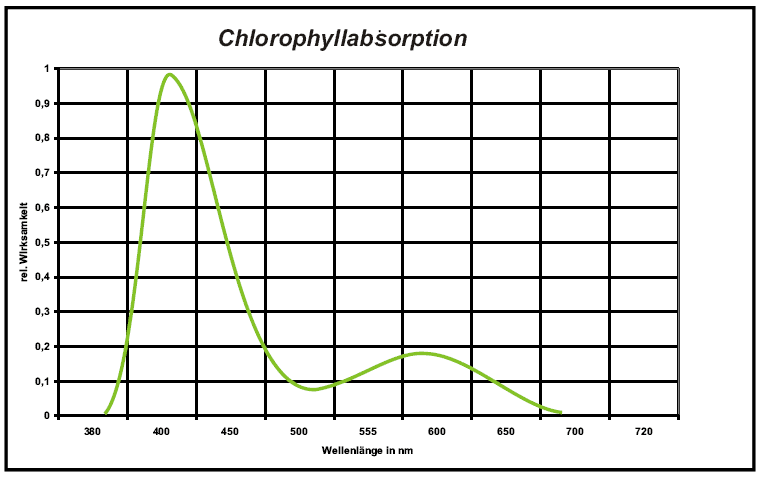
Absorption spectrum of chlorophyll
The actual spectral ranges used by plants for energy transformation have been determined In the course of international research studies. More and more researchers are pushing for sensors rendering the absorption spectrum of plants.
UV-B action spectrum (Caldwell)
This spectral range is part of the ultra-violet light range and has adverse effects on plant growth.
All other action spectra not mentioned here don't have any internationally recognized standardization and the irradiance in their respective frequency spectrum is specified in W/m2. There are no specified standards and integral radiation sensors are hard to find since it's extremely difficult to adjust them using different variations of filters and changing sensitivity.
Spectral range adjusted gauges are very complex, thus being used only sporadically at present.
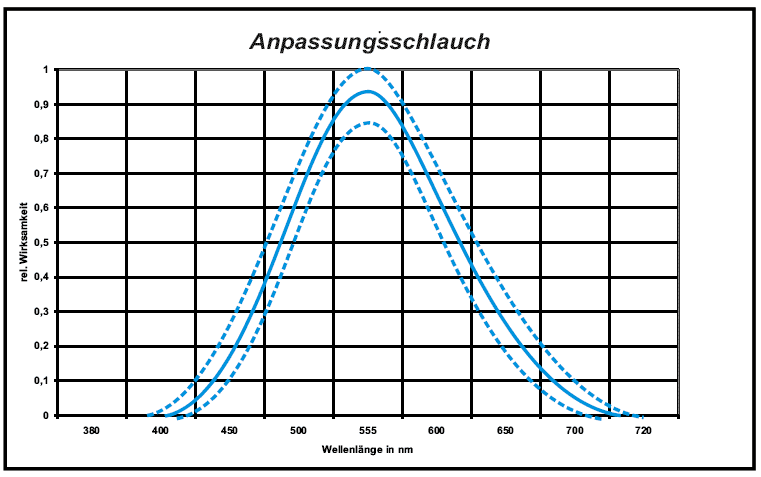
Characteristics of radiation detectors
Spectral distribution
Spectral sensitivity of a sensor should be adjusted to the purpose of measurement, such as measurement of visible light (as explained above). The better the adjustment the more comparable are the results of measuring different radiation sources. Error limits are specified in the standard DIN 5032.(Quality grade L=1,5 %; A=3 %; B=6 %; C=9 %).
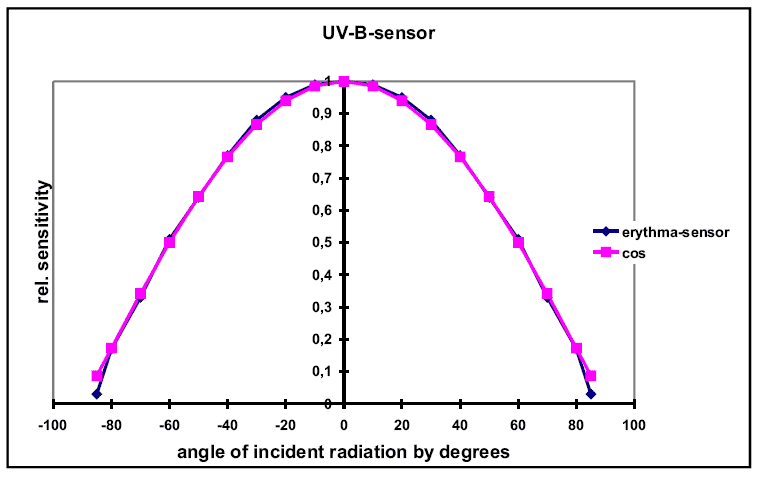
Radiation pattern
In nature radiation always impacts on leveled surfaces, a fact receiving characteristics of a test receiver should comply with. Angular dependancy should have a cosine function.
A photoelectric transformer has to be protected from environmental influences in a housing, that's why certain appliances have to correct measuring data accordingly. The oldest but still most exact method is called integrated sphere. An integrated sphere consists of a hemisphere with a well reflecting inner surface. A small hole allows the light to enter and serves a recipation surface. The light scatters almost infinitely and is measured on an outlet.
New materials such as Polytetrafluoroethylene (PTFE) do have good scattering qualities today, and using an approprate method determined empirically extremely good cosine characteristics can be achieved. Cosine characterisic is tested by rotating the test receiver in 4 metres distance from a point light source.
The allowed integral deviation of a measuring signal from the cosine function is standardized in DIN 5032 as well
(quality class L=1,5%; A=1,5%; B=3%; C=6%).
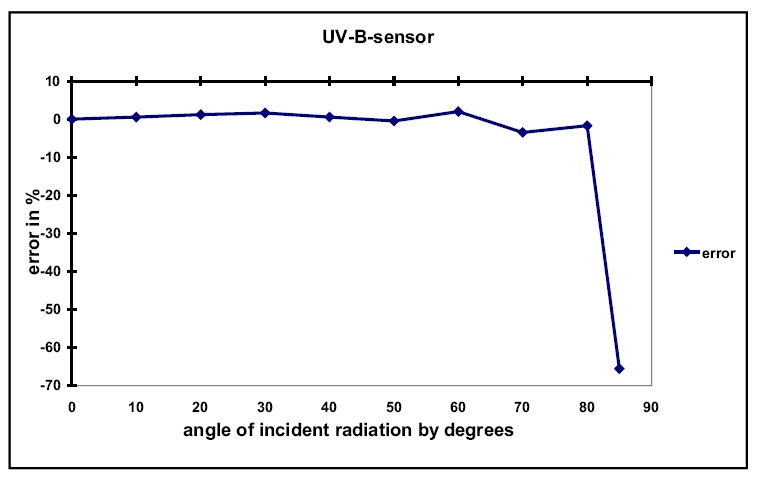
Further error sources
Further errors include linearity, fatigue, temperature coefficient, levelling errors, and the uncertainty of the calibration standards. They are listed in detail in DIN 5032. All errors are cumulated into a single integrated error value ( quality L=3%; A=5%; B=10%; C=20%).
For pyranometers measuring solar and skylight radiation categories are listed in the international standard ISO9060.
Predominant errors are response time (secondary standard < 15s; first class < 30s; second class < 60), Zero off-set response (7W/m²; 15W/m²;30W/m²), change in sensitivity per year (0,8%; 1,5%; 3%), non-linearity (0,5%; 1%; 3%), directional response for beam radiation (10W/m²; 20W/m²; 30W/m²), spectral sensitivity 350 nm to 1,5 µm (2%; 5%; 10%), and temperature response (2%; 4%; 8%).
Calibration of test receivers
Calibration of test receivers is rather tedious without a standard normal of exactly the same type being available. In case there is such a normal it takes just a single light source shining in the spectral range of the sensor and a fixed position, where the normal and the receiver are switched for calibration. Determination of the non-linearity error is simply done by changing distance to the light source.
In case no standard normal is available certain radiation laboratories are equipped with standard normals and monochromators to spatially separate the colors of light.


Absolute sensitivity:
It takes a strong radiation source with a spectral range considerably exceeding the relative spectral sensitivity of the sensor, a line filter with a transmissibility depicting only a small sector of the relative spectral sensitivity, and a calibration photodiode with an exact cosine characteristic.
Relative sensitivity
Relative sensitivity can be determined by placing the sensor into the darkroom of a monochromator measuring station and comparing it to the standard normal nanometer by nanometer. Sensitivity range of the normal has to extend the range of the sensor. Greatest accuracy can be achieved if the range of the measured light is lower than 1 nanomenter and disturbing scattered light can be largely eliminated by e.g. a second monochromator.
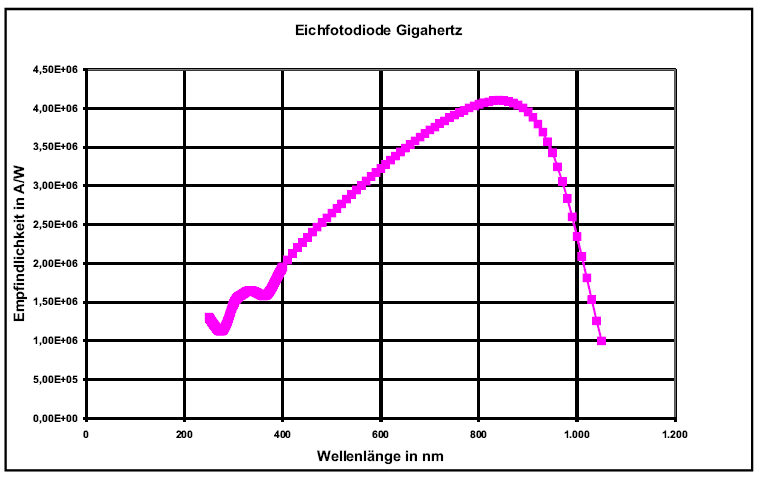
Calibration photodiode
The calibration photodiode used by us is equipped with an extensive plain receiver chip and a housing not altering it's directivity. Now the position of an absolutely exact irradiance has to be determined within the sensitivity range of the sensor. The found position can be used for calibration.
Product Nomenclature



